Geschichte der Warteschlangentheorie

Die mathematische Theorie der Warteschlangen ist noch sehr jung; tatsächlich gibt es sie seit weniger als 100 Jahren. Agner Erlang hat im Jahre 1917 das erste formale Warteschlangenmodell entwickelt, um die Leistung des Telefonsystems (des Internets der damaligen Zeit) zu analysieren. Seine Aufgabe bestand darin, für Amtsgespräche aus Kopenhagen die Puffergröße für Vermittlungen festzulegen. Die heutige Terminologie bezeichnet dieses Modell als Einzel-Warteschlangenmodell.

Einer der nächsten wesentlichen Schritte in der Entwicklung der Warteschlangentheorie folgte 1957, als James Jackson die ersten formalen Lösungen für die Berechnung eines Netzwerks oder einer Kette aus Warteschlangen entwickelte. Dieses Ergebnis blieb 20 Jahre lang rein akademisch, bis man schließlich den Bezug zur Implementierung des Internets erkannte. Das Warteschlangenmodell erwies sich dafür als zutreffend mit einer Abweichung von weniger als fünf Prozent. 1967, etwa fünfzig Jahre nach dem ersten Modell von Erlang, setzte ein Doktorand namens Allan Scherr ein Warteschlangenmodell ein, um die Leistung der CTSS- und Multics-Time-Sharing-Computersysteme zu berechnen, die in vielen Beziehungen die Vorläufer der Unix- und letztendlich damit auch der Linux-Rechner waren.

Fraktale Modelle

In den späten 70er- und frühen 80er-Jahren haben einige neue theoretische Entwicklungen zu vereinfachten Algorithmen für die Berechnung der Leistungsmetriken von Warteschlangensystemen geführt. Diese Algorithmen sind auch in Tools wie PDQ implementiert. Bei den neuesten Entwicklungen in der Warteschlangentheorie geht es um Modelle für den sogenannten selbstähnlichen oder fraktalisierten Paketverkehr im Internet. Diese Begriffe sprengen zwar den Rahmen dieses Artikels; Wer sich aber für weiterführende Informationen interessiert, dem sei Kapitel 10 von [4] empfohlen.

Eine der grundlegenden Annahmen in PDQ ist, dass sowohl die durchschnittliche Zwischenankunftszeit wie die durchschnittliche Bediendauer beide statistisch zufällig sind. Mathematisch gesehen bedeutet das, dass jede Ankunft und jedes Bedienereignis zu einem Poisson-Prozess gehört. Dann entspricht die Dauer dem Mittelwert einer exponentialen Wahrscheinlichkeitsstreuung. Erlang hat festgestellt, dass sich der Verkehr im Telefonnetz tatsächlich dieser Anforderung entsprechend verhält. Es gibt Methoden [5] , mit deren Hilfe sich feststellen lässt, wie gut gegebene Monitoring-Daten diese Anforderung erfüllen.

Wenn diese Monitoring-Daten wesentlich von den Bedingungen des Exponentials abweichen, ist es vielleicht sinnvoller, auf einen ereignisbasierten Simulator wie beispielsweise SimPy [3] auszuweichen, mit dessen Hilfe sich eine größere Bandbreite an Wahrscheinlichkeitsstreuungen berücksichtigen lässt. Das Problem dabei ist, dass die Programmierung und das Debuggen mehr Zeit in Anspruch nehmen (bei jeder Simulation geht es zugleich um die Programmierung); außerdem braucht man länger, um sicherzustellen, dass die Ergebnisse statistisch gültig sind.

Ein weiterer Aspekt, der bei jeder wie auch immer gearteten Vorhersage stört, sind die Fehler, die grundlegende Annahmen des Modells verursachen. Annahmen in Modellen verursachen tatsächlich systematische Fehler im Vorhersageprozess, und daher sollte man sich alle PDQ-Ergebnisse in Wirklichkeit als Streuung plausibler Werte vorstellen. Was außerdem oft unberücksichtigt bleibt, ist die Tatsache, dass jede Quantifizierung fehlerbehaftet ist. Davon sind auch die Monitoring-Daten betroffen – aber wer kennt schon den exakten Fehlerbereich seines Monitoring?

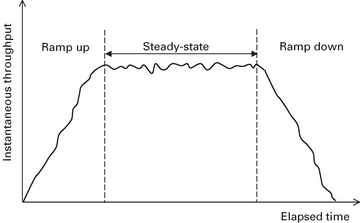
Weil es sich bei allen PDQ-Performance-Ein- und Ausgaben um Durchschnittswerte handelt, ist unbedingt sicherzustellen, dass es sich dabei um zuverlässige Mittelwerte handelt. Die lassen sich beispielsweise in der stabilen Phase (steady state) eines Lasttests messen ( Abbildung 5 ). Der durchschnittliche Durchsatz im stabilen Zustand (X) für eine bekannte Benutzerlast (N) ergibt sich, indem man Messungen über einen längeren Zeitraum T vornimmt und alle Anfahr- oder Herunterfahrzeiten aus den Daten eliminiert. Eine nominelle Zeit T kann beispielsweise fünf bis zehn Minuten betragen, je nach Anwendung. Auch bei Industriestandard-Benchmarks wie SPEC und TPC gilt die Anforderung, dass alle gemeldeten Durchsatzergebnisse aus einem stabilen Zustand stammen.

Abbildung 5: Durchsatzmessungen im stabilen Zustand.